Linear vs nonlinear regression: some things to think about, part 1.

When I started out in statistics, fresh out of college, a general point of confusion was linear versus nonlinear regression modeling. It was easy enough to push a button and analyze data using statistical software, but how was I supposed to interpret the output? What were the mathematical and statistical techniques that the software was using in the background? It all seemed very black box.

In the spirit of the 2019 major league baseball postseason finally coming to an end, I thought it might be worthwhile to briefly touch on this topic (linear versus nonlinear regression modeling) using two common models and a rather simplistic set of baseball data. After providing this example (Part 1), I want to make some general comments regarding how statistical software fits models to your data and why nonlinear modeling can be confusing (Part 2).

In order to come up with a toy example for this post, I visited www.baseball-reference.com and downloaded 2019 regular season pitching game logs for Max Scherzer, ace pitcher for the Washington Nationals. From these game logs, I then selected games in which Scherzer was the starting pitcher and was assigned either a win or a loss (the “pitcher of record”). Here is a select portion of that dataset:

Date	Team		Opponent	Decision	Hits Allowed	Strikeouts
Mar 28	WSN		NYM	L	2	12
Apr 2	WSN		PHI	L	7	9
Apr 7	WSN	@	NYM	W	8	7
Apr 20	WSN	@	MIA	L	11	9
May 1	WSN		STL	L	8	8
May 11	WSN	@	LAD	W	5	7
May 17	WSN		CHC	L	6	8
Jun 2	WSN	@	CIN	W	3	15
Jun 8	WSN	@	SDP	W	6	9
Jun 14	WSN		ARI	W	3	10
Jun 19	WSN		PHI	W	4	10
Jun 25	WSN	@	MIA	W	5	10
Jun 30	WSN	@	DET	W	4	14
Jul 6	WSN		KCR	W	4	11
Sep 8	WSN	@	ATL	W	2	9
Sep 13	WSN		ATL	L	7	6
Sep 18	WSN	@	STL	L	7	11
Sep 24	WSN		PHI	W	5	10

Let’s say I want to ask two questions pertaining to Scherzer’s 2019 performance:

Q1: What’s the relationship between hits allowed and strikeouts?

Q2: What’s the relationship between hits allowed and win/loss decision?

While these questions aren’t particularly important or relevant from a sabermetric standpoint, they do provide a platform for a side-by-side comparison of two basic regression models. Before we get into modeling, however, the respective data are plotted below. (I did drop Scherzer’s first outing from the dataset. I suppose you could justify this since it was his first game of the season and he was settling in to his rhythm for the year, but the only reason I did so was because it provides a better dataset for this illustration.)

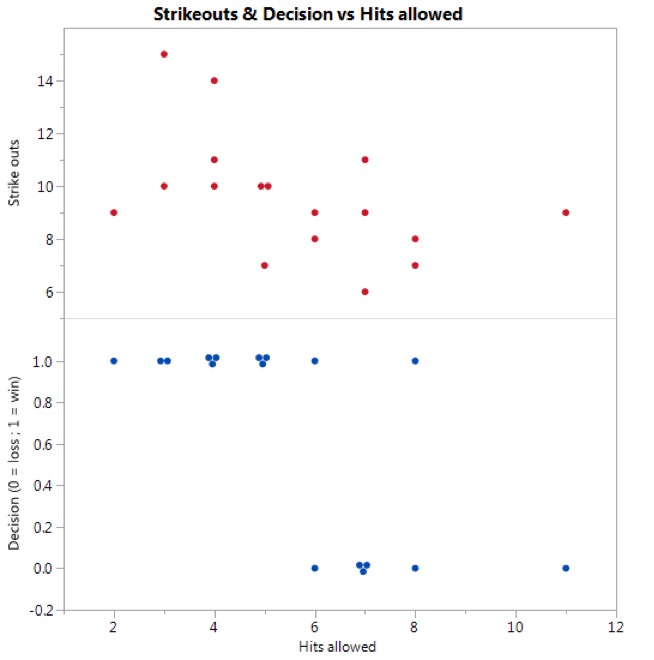
When we look at the data as plotted we can make two observations, both of which are fairly intuitive:

O1: Hits allowed and strikeouts are inversely related to one another. In other words, for any given game, if Scherzer gave up an abnormally high number of hits, then it looks like the total strikeouts for that game were lower than average. Contrapositively, for high strikeout games, it looks like he gave up fewer hits on average.

O2: When we use coded data for win/loss decision, where “1” corresponds to a win and “0” corresponds to a loss, we can also see from the above plot that wins correlate to games in which Scherzer allowed a relatively low number of hits allowed. Losses correspond to a relatively high number of hits allowed.

Ignoring the fact that both strikeouts and hits allowed are discrete numeric variables, we can address Q1 and Q2 using two regression models. (In this case I will assume they are continuous numeric variables. How variable type relates to model selection is a topic for another time.) The specific models we will use are:

M1: The simple linear regression model. We’ll use this to model strike outs.

M2: The simple logistic regression model. We’ll use this to model decision.

For both of these models, “simple” refers to the fact that we are using only one input or predictor variable. In this case, “hits allowed” is the sole input variable we are using to model either decision or strike outs.

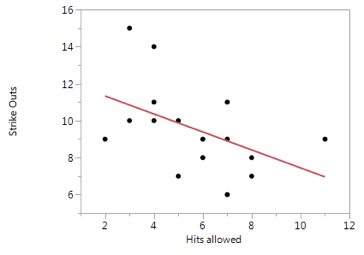
Conceptually, I think M1 is pretty easy to visualize. We essentially have a quantitative response variable (strike outs) and want to model its relationship with another quantitative variable (hits allowed). Use of the term “linear” in M1 communicates that we are going to model this relationship with a straight line as shown below:

M2 is a basic nonlinear regression model that is commonly used for binary response variables. Rather than fitting a straight line through the data as in M1, M2 captures the step change relationship between decision and hits allowed using a nonlinear s-shaped curve:

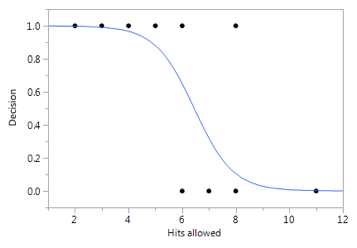
M2 fits our intuition: as hits allowed increases, decision asymptotically approaches “loss.” As hits allowed decreases, decision asymptotically approaches “win.”

Since M1 is simply a straight line through our data, we can easily express this function without much thought:

$M1: Y^{S}_i = \beta^{S}_0 + \beta^{S}_1X_i + \epsilon^{S}_i$

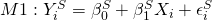
Where 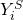$Y^{S}_i$ is the number of strikeouts for game i, 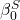$\beta^{S}_0$ is the intercept, 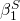$\beta^{S}_1$ is the slope term that relates hits allowed to strikeouts, 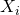$X_i$ is the number of hits allowed for game i, and 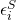$\epsilon^{S}_i$ is the error term. I’m using “S” superscripts to distinguish my strikeout model from my decision model.

M2 takes a little more effort. The logistic model I will use is

$M2: Y^{D}_i = \frac{exp(\beta^{D}_0 + \beta^{D}_1X_i)}{1 + exp(\beta^{D}_0 + \beta^{D}_1X_i)} + \epsilon^{D}_i$

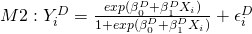
For M2 in particular (“logistic regression”), you’ll often hear people talk about a “link function.” Anytime we model data, we have choices to make: modeling choices that should be justified based on experience, statistical theory, or hopefully a little bit of both. Whenever we use logistic regression, we have options for expressing the exact nonlinear functional relationship between X and Y. For M2 as it is written above, I used a popular link function known as the logit link. For now, without going into all the details of how to interpret the M2 parameters, think of this as a model for estimating the probability of a “win” decision as highlighted in Figure 3.

Since we now have models that can be applied to our dataset, we can use software to come up with respective parameter estimates. I used JMP to analyze these data and came up with the following estimates:

For M1: 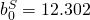$b^S_0 = 12.302$ ; $b^S_1 = - 0.486$

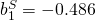
For M2: 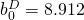$b^D_0 = 8.912$ ; $b^D_1 = - 1.381$

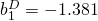
We could then use these estimates to make predictions if we so desired. Suppose we watch a game in which Scherzer allows 7 hits. On average we might reasonably expect

12.302 – 0.486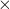 $\times$ 7 = 8.9 strikeouts and a

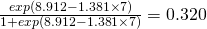$\frac{exp(8.912 - 1.381\times 7)}{1 + exp(8.912 - 1.381\times 7)} = 0.320$ probability of being assigned a win*.

Having fit two rather simplistic regression models to our dataset, one linear and one nonlinear, in Part 2 I want to discuss some more general considerations. How are model estimates calculated? Does the type of model matter?

For now I’ll conclude by saying: go Nats!

*Assuming he is the pitcher of record. Like I said before, this particular example isn’t overly insightful in terms of its practicality.

Linear vs nonlinear regression: some things to think about, part 1. - Stat Nuggets